Intensità efficace della corrente alternata

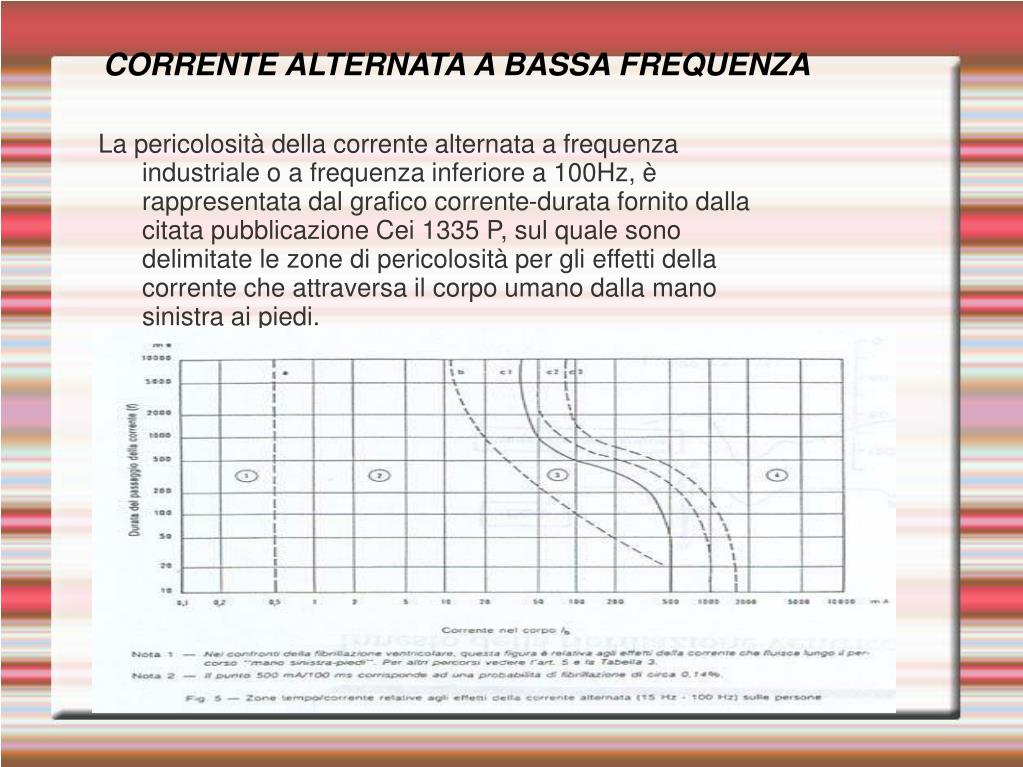
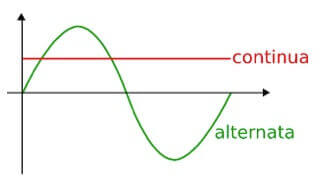
Per intensità efficace di una corrente alternata si intende quel valore di corrente che, attraversando una resistenza elettrica, produrrà lo stesso effetto termico di una corrente continua.

Applicando la legge di Joule ad una corrente continua ${\displaystyle I}$ che attraversa una resistenza ${\displaystyle R}$, tale corrente compirà un lavoro elettrico ${\displaystyle L_{cc}}$ atto a produrre in un intervallo di tempo ${\displaystyle t}$ una quantità di energia pari a:

${\displaystyle L_{cc}=I^{2}\,R\,t}$

Allo stesso modo una corrente in regime sinusoidale con valor massimo ${\displaystyle I_{M}}$, attraversando la stessa resistenza ${\displaystyle R}$, con andamento ${\displaystyle i=I_{M}\,\sin(\omega t)}$ e potenza istantanea ${\displaystyle P=i^{2}\,R}$ nell'intervallo di tempo del semiperiodo ${\displaystyle T/2}$, dove la corrente ha verso costante, avrà effettuato un lavoro ${\displaystyle L_{ca}}$ di:

${\displaystyle L_{ca}=\int _{0}^{\frac {T}{2}}I_{M}^{2}\,R\,\sin ^{2}(\omega t)\,dt\quad \Rightarrow \quad L_{ca}=I_{M}^{2}\,R\int _{0}^{\frac {T}{2}}\sin ^{2}(\omega t)\,dt}$

Effettuiamo a questo punto una sostituzione di variabile ponendo:

${\displaystyle x=\omega t\quad t={\frac {x}{\omega }}\quad \Rightarrow \quad dt={\frac {dx}{\omega }}\quad \Rightarrow \quad L_{ca}={\frac {I_{M}^{2}\,R}{\omega }}\int _{0}^{\frac {T}{2}}\sin ^{2}(x)\,dx}$

Essendo ${\displaystyle \sin ^{2}(x)\,dx}$ un integrale rilevante, ne è conosciuta la soluzione:

${\displaystyle \int \sin ^{2}x\,dx={\frac {1}{2}}{\Bigl (}x-\sin x\,\cos x{\Bigr )}}$

Applicandola:

${\displaystyle L_{ca}={\frac {I_{M}^{2}\,R}{2\omega }}{\Bigl [}x-\sin x\,\cos x{\Bigr ]}_{0}^{\frac {T}{2}}}$

Risostituendo ${\displaystyle x}$ e tenendo conto del valore della velocità angolare ${\displaystyle \omega }$ del vettore corrente:

${\displaystyle x=\omega t\quad \omega ={\frac {2\pi }{T}}\quad x={\frac {2\pi }{T}}t\quad con:\ t={\frac {T}{2}}\to x={\frac {2\pi }{T}}{\frac {T}{2}}=\pi \quad con:\ t=0\to x={\frac {2\pi }{T}}0=0}$

Quindi nel calcolo:

${\displaystyle L_{ca}={\frac {I_{M}^{2}\,R}{2\omega }}{\Bigl [}(\pi -\sin \pi \,\cos \pi )-(0-\sin 0\,\cos 0){\Bigr ]}={\frac {I_{M}^{2}\,R}{2\omega }}\pi \quad {\frac {\pi }{\omega }}={\frac {T}{2}}\quad L_{ca}={\frac {1}{4}}I_{M}^{2}\,R\,T}$

Dovendo essere l'energia termica prodotta nell'intervallo del semiperiodo ${\displaystyle T/2}$ uguale sia per la corrente continua che per l'alternata, anche i lavori elettrici devono coincidere ${\displaystyle (L_{cc}=L_{ca})}$ e, stabilito per definizione che il valore della corrente continua rappresenta il valore efficace ${\displaystyle I_{e}}$ sarà:

${\displaystyle L_{cc}=I_{e}^{2}\,R{\frac {T}{2}}\qquad {\frac {1}{2}}I_{e}^{2}\,R\,T={\frac {1}{4}}I_{M}^{2}\,R\,T\qquad 2I_{e}^{2}=I_{M}^{2}\qquad I_{e}={\frac {I_{M}}{\sqrt {2}}}}$

Valore efficace della tensione alternata

Analogamente a quanto visto per la corrente possiamo determinare il valore efficace per la tensione seguendo la logica:

${\displaystyle L_{cc}={\frac {V^{2}}{R}}t\qquad v=V_{M}\,\sin(\omega t)\qquad L_{ca}={\frac {V_{M}^{2}}{R}}\int _{0}^{\frac {T}{2}}\sin ^{2}(\omega t)\,dt\qquad {\frac {V_{e}^{2}}{R}}{\frac {T}{2}}={\frac {V_{M}^{2}}{R}}{\frac {T}{4}}\qquad V_{e}={\frac {V_{M}}{\sqrt {2}}}}$

Voci correlate

• Corrente alternata
• Corrente continua
• Effetto Joule
• Potenza elettrica
• Energia
• Velocità angolare